Die Vielseitigkeit von Phi

Der Goldene Schnitt ist ein Maßverhältnis, das von Menschen verschiedener Kulturkreise seit jeher als harmonisch und angenehm empfunden wird und bei Strecken- und Flächenteilungen sowie Formproportionen auftritt. Kaum ein anderes Maßverhältnis warf zugleich so viele Rätsel auf und erstaunte durch sein überraschend häufiges und facettenreiches Auftreten in verschiedensten gestalterischen, naturwissenschaftlichen und spirituellen Gebieten. Immer wieder setzten sich damit Künstler, Architekten und Mathematiker damit auseinander.

Dieses besondere Teilungsverhältnis faszinierte die Menschen schon lange vor seiner ersten schriftlichen Erwähnung im zweiten Buch der „Elemente“ des griechischen Mathematikers Euklid (365 – 300 v. Chr.). Dort lesen wir als 11. Satz die folgende Aufgabe: „Eine gegebene Strecke ist so zu teilen, dass das Rechteck aus der ganzen Strecke und dem einen Abschnitt dem Quadrat über dem anderen Abschnitt gleich ist. Mit anderen Worten:Der Goldene Schnitt ist eine spezielle Teilung einer Strecke, bei der die ganze Strecke zum längeren Abschnitt im selben Verhältnis steht, wie die kürzere Strecke zur längeren„

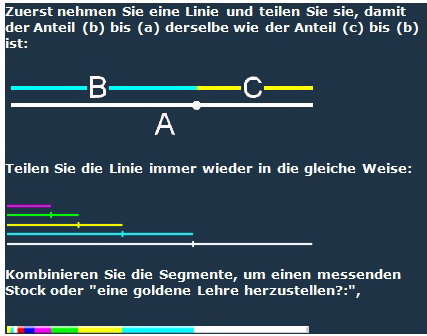
Der goldene Schnitt ist ein ganz besonderes Teilungsverhältnis. Nehmen wir mal an, es sei eine Strecke gegeben, etwa zwischen zwei Punkten A und B. (Für die Strecke schreiben wir dann [A,B]; ihre Länge bezeichnen wir mit AB.) Ist noch ein weiterer Punkt S gegeben, der auf der Strecke [A,B] liegt, so teilt S [A,B] in zwei kleinere Abschnitte. Man sagt S teilt [A,B] im goldenen Schnitt, wenn das Verhältnis des kleineren zum größeren dieser Abschnitte genauso groß ist, wie das Verhältnis des größeren Abschnitts zur ganzen Strecke.

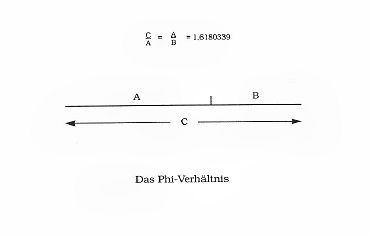
Der goldene Abschnitt ist ein Verhältnis gegründet auf einem Phi. Das Verhältnis Zahl Phi ist eine Proportion. Wenn man eine beliebige Strecke C unterteilt im Verhältnis Phi = 1.6180339…, dann sind auch die Strecken C/A und A/B im Verhältnis Phi geteilt.

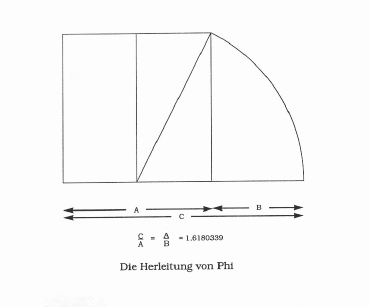
Zur geometrischen Herleitung von Phi teilt man ein Quadrat vertikal in der Mitte und zieht eine Diagonale in einen der beiden Rechtecke. Mit der Diagonale als Radius schlägt man einen Kreisbogen zur Basis-Linie. Die Basis-Linie ist nun geteilt im Verhältnis Phi und es gilt C/A und A/B = 1.6180339…. .

In der Renaissance war dieser „goldene Abschnitt“ als „Divine Anteil“ bekannt. Sie verwendeten ihn für die Schönheit und Abgleichung in der Kunst und im Design.

 

Ihre Existenz und Aktualität finden wir in vielen Beispielen der Kunst, der Architektur, in Designs wieder. Als aktuelles Beispiel soll hier Notre Dame genannt sein.

 

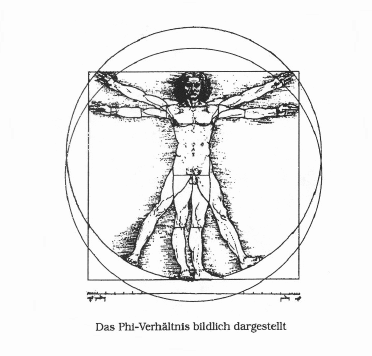
Man kann den menschlichen Körper auch in einen Kreis setzen, dessen Zentrum sich dann am Bauchnabel befindet. Das Quadrat und der Kreis treffen sich an den Füßen, wobei der Abstand Nabel Steißbein genau halb so groß ist wie der Abstand zwischen höchstem Punkt des Kopfes und dem äußeren Kreisrand. Verschiebt man das Zentrum des Kreises vom Nabel zum Steißbein, erhält man wieder das Bild des Phi-Verhältnisses.

  

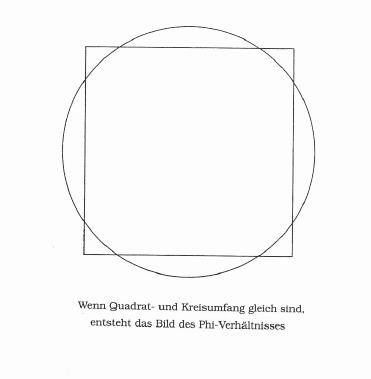
Das Phi-Verhältnis entsteht immer dann, wenn Umfang von Kreis und Quadrat gleich sind. Um auf mathematischem Weg Phi herzuleiten, kann man auf diese Weise einen Körper in einen Kreis setzen und in der Mitte durch eine Achse in Nord-Süd Richtung teilen.

  

Wir finden die Anwendung des „goldenen Abschnitts“ in der Natur, in den Bewegungen der Börse und in vielen anderen Aspekten des Universums. Heute ist bekannt, dass der goldene Abschnitt – Devine-Anteil – sich in bestimmten Anteilen des lebenden Organismus darstellt. Es erstaunte mich schon, als ich die räumliche und zeitliche Unveränderlichkeit erkannte und wie vielseitig ihre Anwendung sein kann.

                                        

Für mich stellte sich die Frage: Kann der „Goldenen Abschnitt“ zu einem goldenen Rasterfeld erweitert werden? nach langen Recherchen kan ich diese Frage mit einem klaren – Ja – beantworten.

Ich habe ein Rasterfeld kreiert, das metrisch im Design zum lebenden Organismus ist. Das ist die Antwort auf meine Frage.