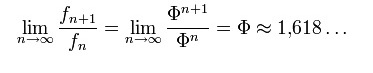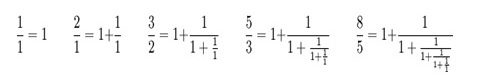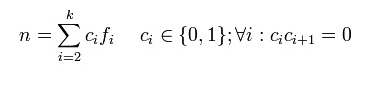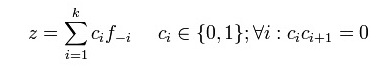Die Beschreibung dieses Anteils als „Goldenes“ und „Divine“ passt möglicherweise, weil viele Menschen sie als Tür sehen, die zu einem tieferen Verständnis für Schönheit und zur Spiritualität im Leben führt. Es ist schon unglaublich, welche Rolle diese eine Zahl in der menschlichen Geschichte und im Universum spielt. Es dauerte nicht lange und ein Mann namens Leonardo da Pisa, auch Leonardo Fibonacci genannt, die Zahlenreihe „Phi“. Fibonacci war einer der bedeutendsten Mathematiker des Mittelalters und lebte in Pisa.

      

12. Jahrhundert entdeckte Leonardo Fibonacci eine einfach numerische Reihe, die die Grundlage für ein unglaubliches mathematisches Verhältnis hinter „Phi“ ist. Beginnend mit „0″ und „1″ ist jede neue Zahl in der Reihe einfach die Summe 2 vor ihr. Z.B.:  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Er beschrieb damals die Fortpflanzung, die Vermehrung von Kaninchen. Was ich nicht verschweigen will ist, dass in Indien und in der westlichen Antike diese Zahlenfolge schon bekannt war. Das Verhältnis jedes aufeinanderfolgenden Paares Zahlen in der Reihe approximiert „Phi“ (1,618. ) als 5 geteilt durch 3 ist 1,666… und 8 geteilt durch 5 ist 1,60.  Die nachfolgend aufgeführte Tabelle, wie die Verhältnisse der aufeinanderfolgenden Zahlen in der Fibonacci-Folge schnell auf Phi zusammenlaufen, oder ¦. Nach der 40th Zahl in der Reihe ist das Verhältnis zu 15 Dezimalstellen genau: 1,618033988749895

Ihr könnt jede mögliche Zahl in der Fibonacci-Folge leicht berechnen! Verwendet „Phi“, um die nth- Zahl in der Fibonacci-Folge (f N) zu berechnen: f n = ¦ ½ n/ 5 (dieses liefert eine Schätzung, die immer zur korrekten Fibonaccizahl rundet). Das Verhältnis der aufeinanderfolgenden Fibonaccizahlen läuft auf Phi hinaus.

Die Fibonacci-Folge ist  durch das rekursive Bildungsgesetz

Das rekursive Bildungsgesetz in der Mathematik ist eine Auflistung (Familie) von endlich oder unendlich vielen fortlaufend nummerierten Objekten (beispielsweise Zahlen) bezeichnet. Dasselbe Objekt kann in einer Folge auch mehrfach auftreten. Das Objekt mit der Nummer i, man sagt hier auch: mit dem Index i, wird i-tes Glied oder i-te Komponente der Folge genannt.

mit den Anfangswerten

definiert.

 

Das bedeutet in Worten:

• Für die beiden ersten Zahlen werden die Werte null und eins vorgegeben.
• Jede weitere Zahl ist die Summe ihrer beiden Vorgänger.

 

Oft wird auch f₀ = 0 ausgelassen und die Fibonacci-Folge mit f₁ = 1 und f₂ = 1 beginnend definiert, insbesondere bei der Anwendung auf Situationen, in denen ein Anfangswert Null keinen Sinn hat. Die Folge kann über die Rekursion (lat. recurrere „zurücklaufen. So wird wird eine Technik in der Mathematik, Logik und Informatik bezeichnet – eine Funktion durch sich selbst zu definieren).

Auch der Bereich mit negativem Index n erweitert kann werden.Es gilt:

Die in den negativen Indexbereich erweiterte Fibonacci-Folge lautet dann:

Darüber hinaus ist eine Verallgemeinerung der Fibonacci-Zahlen auf komplexe Zahlen und auf Vektorräume möglich.

 

Eigenschaften:

Beziehungen zwischen den Folgegliedern

Identität von Catalan:
Besondere Zahlen sind zum einen Zahlen, die im Sinne der Zahlentheorie eine oder mehrere auffällige Eigenschaften besitzen. Außerdem haben viele Zahlen eine besondere Bedeutung in der Mathematik und/oder in Bezug auf die reale Welt. Diese letzteren Zahlen werden im zweiten Teil dieses Artikels aufgelistet.

 

Identität von Casini, d’Ocagne und Catalan:
Cassini-, d’Ocagne– und die katalanische Identität sind mathematische Identitäten für die Fibonacci-Zahlen . Das erstere ist ein spezieller Fall der letzteren, und erklärt, dass für die n-te Fibonacci-Zahl.

 

Spannend sind auch die nachfolgend aufgeführten Identitäten, Theorien u.a.:
Brown Criterion, Fast-Fibonacci Transform, Fibonacci Dual-Theorem, Fibonacci n-Step-Nummer, Fibonacci Polynomial , Fibonacci Prime, Fibonacci Q-Matrix , Fibonomial Coefficient, Fibonorial, Gelin-Cesaro Identität, Generalized Fibonacci-Zahl, Inverse Tangent , Linear Rekursionsgleichung, Lucas Sequence, der Umgebung von Noble Anzahl, Pell-Nummer, Pisano Zeitraum, Kaninchen Constant, Zufalls-Fibonacci Sequence , gegenseitige Fibonacci Constant , Stolarsky Array, Tetranacci Anzahl, Tribonacci Anzahl, Wythoff Array, Zeckendorf Vertretung, Zeckendorf Theorem

 

Eines von Johannes Keppler`s Theorie zeigen eine Verwandtschaft mit dem Goldenen Schnitt auf.

Wie von Johannes Kepler festgestellt wurde, nähert sich der Quotient zweier aufeinander folgender Fibonacci-Zahlen dem Goldenen Schnitt Φ an. Dies folgt unmittelbar aus der Näherungsformel für große n:

Diese Quotienten zweier aufeinander folgender Fibonacci-Zahlen haben eine bemerkenswerte Kettenbruchdarstellung:

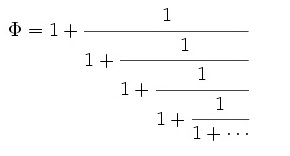
Da diese Quotienten im Grenzwert gegen den goldenen Schnitt konvergieren, lässt sich dieser als der unendliche Kettenbruch darstellen:

Φ ist eine irrationale Zahl. Das bedeutet, dass sie sich nicht durch ein Verhältnis zweier ganzer Zahlen darstellen lässt, ein Umstand, der wesentlich zu ihrer Bedeutung in Kunst und Natur beiträgt. Am besten lässt sich Φ durch Quotienten zweier aufeinander folgender Fibonacci-Zahlen darstellen. Dies gilt auch für verallgemeinerte Fibonaccifolgen, bei denen f₀ und f₁ beliebige natürliche Zahlen annehmen.

Zeckendorf-Theorem

Das Zeckendorf-Theorem, dass jede natürliche Zahl n größer Null eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen geschrieben werden kann. Das heißt, es gibt für jedes 0″ height=“18″ width=“106″>eine eindeutige Darstellung der Form

Die entstehende Folge (c)_i von Nullen und Einsen wird Zeckendorf-Sequenz genannt. Da aufeinanderfolgende Fibonacci-Zahlen ausgeschlossen sind, können keine zwei Einsen in einer Zeckendorf-Sequenz unmittelbar hintereinander stehen. Allgemeiner ist die verwandte Aussage, dass sich jede ganze Zahl z eindeutig als Summe verschiedener, nicht direkt aufeinanderfolgender negaFibonacci-Zahlen (f _{− k} mit ) darstellen lässt.

So wäre zum Beispiel − 2 = f _{− 1} + f _{− 4} = 1 − 3 als Binärsequenz 1001 darstellbar.