Bevölkerungswachstum ist auch mit der Fibonacci Reihe verbunden.
Fibonacci schrieb zwar über eine Vielzahl mathematischer Themen, doch ist er in erster Linie wegen der Zahlenfolge 1, 1, 2, 3, 5, 8, 13, 21 … bekannt. Die Folge wurde später nach ihm benannt und ist heute noch Gegenstand reger Forschungstätigkeit. Eine beliebige Zahl dieser Folge ergibt sich durch die Addition der beiden vorhergehenden Zahlen: Fn = Fn-1 + Fn-2. Als Ausgangspunkte dienen F1 = 1 und F2 = 1. Ihren Ursprung hat diese Zahlenfolge in einem eher trivialen Problem, einer von vielen Rechenaufgaben, die Fibonacci in seinem Liber abaci behandelt: der sogenannten Kaninchenaufgabe. Bei Fibonacci selber ist allerdings die erste 1 der Folge nicht berücksichtigt.
Fibonacci konnte schon damals die Population der Kaninchen berechnen. Ob dies auch auf die menschliche Spezies anzuwenden ist, rechnet einfach mal. Doch zurück zu den Kaninchen, Fibonacci und der Vermehrung der Kaninchen. Er stellte sich die Frage, wie schnell Kaninchen unter sich unter idealen Verhältnissen fortpflanzen können. Man schrieb das Jahr 1202, als Vibonacci diese Frage versuchte zu beantworten. Es war die Frage dessen, wie sich schnelle Kaninchen unter idealen Verhältnissen fortpflanzen konnten, die Leonardo Fibonacci ursprünglich das Jahr 1202 untersuchte. Hier war die Frage, die er stellte: “Wie viele Kaninchenpaare entstehen im Verlauf eines Jahres aus einem Paar?
Das Experiment:
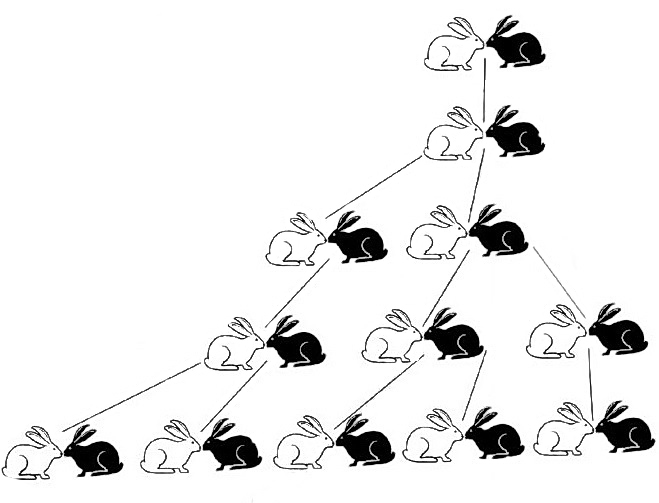
„Ein Mann hielt ein Paar Kaninchen an einem Ort, der ringsum von einer Mauer umgeben war, um herauszufinden, wie viele Paare daraus in einem Jahr entstünden. Dabei ist es ihre Natur, jeden Monat ein neues Paar auf die Welt zu bringen, und sie gebären erstmals im zweiten Monat nach ihrer Geburt. Weil das obengenannte Paar schon im ersten Monat gebiert, kannst du es verdoppeln, so dass nach einem Monat zwei Paare da sind. Von diesen gebiert eines, d.h. das erste, im zweiten Monat wieder; und so gibt es im zweiten Monat 3 Paare. Von denen werden in einem Monat 2 wieder trächtig, so dass im dritten Monat zwei Kaninchenpaare geboren werden; und so sind es dann in diesem Monat 5 Paare. Von denen werden im selben Monat 3 trächtig, so dass es im vierten Monat 8 Paare sind. Von diesen gebären 5 Paare wieder 5 Paare; wenn man diese zu den 8 Paaren addiert, ergeben sich im fünften Monat 13 Paare. Von denen paaren sich die 5 Paare, die in diesem Monat geboren wurden, noch nicht im selben Monat, aber die anderen 8 Paare werden trächtig; und so sind es im sechsten Monat 21 Paare. Wenn man zu diesen die 13 Paare addiert, die im siebten Monat geboren werden, werden es in diesem Monat 34 Paare sein. Wenn man zu diesen die 21 Paare addiert, die im achten Monat geboren werden, werden es in diesem Monat 55 Paare sein. Wenn man zu diesen die 34 Paare addiert, die im neunten Monat geboren werden, werden es in diesem Monat 89 Paare sein. Wenn man zu diesen wiederum die 55 Paare addiert, die im zehnten Monat geboren werden, werden es in diesem Monat 144 Paare sein. Wenn man zu diesen wiederum die 89 Paare addiert, die im elften Monat geboren werden, werden es in diesem Monat 233 Paare sein. Und wenn man schließlich zu diesen die 144 Paare addiert, die im letzten Monat geboren werden, sind es am Schluss 377 Paare. Und so viele Paare wird das obengenannte Paar an dem beschriebenen Ort am Ende eines Jahres auf die Welt gebracht haben…“
Quelle: Deutsche Übersetzung aus dem 12. Kapitel des Liber abaci nach der lateinischen Edition von B. Boncompagni, Rom 1857, S. 283f. Signatur 73155:1
| Monat | Hase A: | Hase B: | Hase C: | D: | B1: | Total | ||||||||
| 0 | A | 1 | ||||||||||||
| 1 | A | 1 | ||||||||||||
| 2 | A | B | 2 | |||||||||||
| 3 | A | B | C | 3 | ||||||||||
| 4 | A | B | C | D | B1 | 5 | ||||||||
| 5 | A | B | C | D | E | B1 | B2 | C1 | 8 | |||||
| 6 | A | B | C | D | E | F | B1 | B2 | B3 | C1 | C2 | D1 | B11 | 13 |
| etc. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | etc |
Die Fibonacci-Reihe können verwendet werden, um die städtische Bevölkerung vorhersagen:
| Volkszählung Rang | aktuelle Bevölkerung | progn. Bevölkerung | ||
| Methode 1 | Methode 2 | |||
| New York, NE NJ | 1 | 16,206,841 | ||
| LA Long Beach CA | 2 | 8,351,266 | 10,016,379 | 10,016,379 |
| Chicago NW IN | 3 | 6,714,578 | 6,190,462 | 5,161,366 |
| Detroit, MI | 5 | 3,970,584 | 3,825,916 | 4,149,837 |
| Washington DC | 8 | 2,481,459 | 2,364,546 | 2,453,956 |
| Houston, TX | 13 | 1,677,863 | 1,461,370 | 1,533,626 |
| Cincinnati, OH | 21 | 1,110,514 | 903,176 | 1,036,976 |
| Dayton, OH | 34 | 685,942 | 558,194 | 686,335 |
| Richmond, VA | 55 | 416,563 | 344,983 | 423,935 |
| Las Vegas, NV | 89 | 236,681 | 213,211 | 257,450 |
| New London, CT | 144 | 139,121 | 131,772 | 146,277 |
| Great Falls, MT | 233 | 70,905 | 81,439 | 85,982 |
Die Methode 1 nimmt die Bevölkerung der größten Stadt und teilt es immer wieder durch Phi. Methode 2 nimmt die Bevölkerung jeder aufeinander folgenden Stadt und teilt es durch Phi.
Mehrzelligen Organismen:
Sobald ein Ei befruchtet wird, teilt und vermehrt es sich und multipliziert in der Zählung, bis es einen Punkt erreicht, an dem das Verhältnis der folgenden Zahl von Zellen zur vorherigen Zahl von Zellen Phi (1.618…) ist.