Phi definiert unser Leben in der Mathematik und Physik. Phi fährt fort, neue Türen in unserem Verständnis des Lebens und des Universums zu öffnen. Roger Penrose machte in den siebziger Jahren die Entdeckung der „Penrose-Parkettierung”, die erlaubte, dass Oberflächen in der fünffachen Symmetrie mit Ziegeln gedeckt werden. Phi als Tür Die Beschreibung dieses Anteils als „Goldenes“ und „Divine“ passt möglicherweise, weil viele Menschen Phi als Tür sehen, die zu einem tieferen Verständnis für Schönheit und zur Spiritualität im Leben führt. Es ist schon unglaublich, welche Rolle diese eine Zahl in der menschlichen Geschichte und im Universum spielt.

Während der Geschichte wurde Phi immer wieder entdeckt und neu entdeckt. Das erklärt auch, warum Phi in den verschiedensten Epochen andere Namen bekam.  Schon die alten Griechen und Ägypter benutzen Phi in ihrer Architektur. Die Ägypter (Egytians) verwendete PU und Phi im Design der großen Pyramiden. Der Grieche, der Phi den goldenen Abschnitt nannte, gründete das gesamte Design des Parthenon auf diesem göttlichen Anteil. Phidias (500 BC – 432 BC), ein griechischer Sculptor und ein Mathematiker, studierte Phi. Plato (circa 428 BC – 347 BC), in seinen Ansichten über natürliche Wissenschaft und das Cosmology, die in seinem “Timaeus“ dargestellt wurde, betrachtete den goldenen Abschnitt, die meiste Schwergängigkeit aller mathematischen Verhältnisse und des Schlüssels zur Physik des Cosmos zu sein. Euclid (365 BC – 300 BC), in den Elementen, bezogen eine Linie am 0,6180399… Punkt als Teile einer Linie im Übermaß und im Mittelverhältnis teilend. So wurde die Bezeichnung: „im goldenen Mittel“ kreiert. Er verband auch diese Zahl mit dem Aufbau eines Pentagram.

Die Fibonacci-Folge wurde im Jahr 1200 entdeckt.
Leonardo Fibonacci, ein Italiener, geboren im Jahr 1175, entdeckte die ungewöhnlichen Eigenschaften der numerischen Reihe, die jetzt seinen Namen führt, aber es ist nicht sicher, dass er sogar seinen Anschluss zum Phi und zum goldenen Mittel verwirklichte. Sein bemerkenswertester Beitrag zur Mathematik war eine Arbeit, die als Rechenmaschinen Liber bekannt ist, die Angeleinfluss in der Annahme durch die Europäer des arabischen dezimalen Systems des Zählens der römischen Übermäßigziffern wurden.

Im 15. Jahrhundert wurde erstmals der “Divine Anteil” erwähnt.
Da Vinci stellte Abbildungen für eine Abhandlung zur Verfügung, die veröffentlicht wurde von Luca Pacioli in 1509 erlaubt “De Divina Proportione” (1), möglicherweise den frühesten Hinweis in der Literatur zu anderen seiner Namen, der “Divine Anteil.”, Dieses Buch enthält die Zeichnungen, die durch Leonardo Da Vinci der fünf Körper Platonic gebildet werden. Es war vermutlich Da Vinci, der es zuerst das “sectioaurea“ nannte, das für goldenen Abschnitt lateinisch ist. Die Renaissancekünstler verwendeten das goldene Mittel weitgehend in ihren Anstrichen und in Skulpturen, Abgleichung und Schönheit zu erzielen. Leonardo Da Vinci zum Beispiel verwendete es, um alle grundlegenden Anteile seinem Anstrich “das letzte Abendmahl, ” von den Maßen der Tabelle zu definieren, an der Christ und die disciples zu den Anteilen den Wänden und den Fenstern im Hintergrund saßen. Johannes Kepler (1571-1630), Entdecker der elliptischen Natur der Bahnen von den Planeten um die Sonne, sagte: “Geometrie hat zwei große Schätze: eins ist das Theorem von Pythagoras; die andere, die Abteilung einer Linie in Extremes und Mittelverhältnis. Das erste können wir mit einem Maß Gold vergleichen; die Sekunde können wir ein kostbares Juwel nennen.”, Mit  „Phi“ wurde bis Anfang des 1900 Jahrhundert gerechnet.  Bis zu dieser Zeit war bekannt, dass dieser überall vorhandene Anteil als der „goldene Mittel-, goldene Abschnitt und/oder das goldene Verhältnis“, sowie den „Divine Anteil“bezeichnet wird. „Phi“ ist der erste Buchstabe von Phidias, der das „goldene Verhältnis“ in seinen Skulpturen verwendete, sowie das griechische Äquivalent zum Buchstaben “F,” Der erste Buchstabe von Fibonacci. Der Buchstabe für Phi jedoch hat auch einige interessante theologische Implikationen.

 

Wie kann Phi mathematisch abgeleitet werden:

Schaut Euch diese Gleichung an:

² – n ¹ – n ⁰ = 0
ist das gleiche wie
n ² – n – 1 = 0

Sie könnte auch heißen:

n ² = n + 1 und 1/n = n – 1

Die Lösung der Gleichung: Quadratwurzel von 5 plus 1 geteilt durch 2:

(5^1/2 + 1) /2 = 1,6180339… = Phi

 

Dieses ergibt selbstverständlich zwei Eigenschaften, die zum Phi einzigartig sind.
Wenn Sie Phi quadrieren, erhalten Sie eine Zahl genau 1 grösser als Phi: 2,61804…

Phi ² = Phi + 1

Wenn Sie Phi in 1 teilen, erhalten Sie eine Nr. genau 1 weniger als Phi: 0,61804…

1 / Phi= Phi – 1

Phi kann auch beschrieben werden

5 ^ .5 * .5 + .5 = Phi

Bestimmung der nth-Zahl in der Fibonacci-Folge:

Sie können Phi verwenden, um die nth-Zahl in der Fibonacci-Folge (f N) zu berechnen:

f _n = Phiⁿ / 5^1/2

Als Beispiel ist die 40th Zahl in der Fibonacci-Folge 102, 334, 155, die wie berechnet werden kann:

f ₄₀ = Phi ⁴⁰ / 5^1/2 = 102.334.155

Diese Methode liefert wirklich nur eine Schätzung, die sich immer zur korrekten Fibonaccizahl rundet. Sie können jede mögliche Zahl der Fibonacci-Folge (f N) genau berechnen mit einer wenig mehr Arbeit:

f _n = [ Phi ⁿ – (- Phi) ^{– n} ] / (2 Phi-1)

Anmerkung:

2 Phi -1 = 5 ^1/2 = die Quadratwurzel von 5

Bestimmung von Phi mit der Trigonometrie:

Phi kann mit dem Pi durch trigonometrische Funktionen verbunden sein.
2^. cos (π : 5) = ø oder 2^. sin (π : 5) = √ 3 – ø

Phi kann in Verbindung gesetzt zu e, durch die umgekehrte hyperbolische Sinus-Funktion berechnet werden.

Phi = e ^ asinh(.5)

Andere „ungewöhnliche“ Beziehungen zu Phi:

Es gibt viele ungewöhnliche Beziehungen in der Fibonacci-Reihe. Zum Beispiel für alle drei Zahlen in der Reihe:  Phi (n-1), Phi (n) und Phi (n +1), besteht folgender Zusammenhang:

                                                            Phi(n-1) * Phi(n+1) = Phi(n)² – (-1)ⁿ

 

Eine andere „ungewöhnliche Beziehung“:

Jede n-te Fibonacci-Zahl ist ein Vielfaches von Phi (n), wo Phi (n) ist die n-te Zahl in der Fibonacci-Folge.

Betrachten wir die Zahlen:

0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765    

(Jede 4. Zahl ist ein Vielfaches von Phi (4). Z. B: 3, 21, 144 und 987 – ergibt die Zahl 3)

(Jede 5. Zahl ist ein Vielfaches von Phi: z.B: 5, 55. 610, 6765 – ergibt die Zahl: 5)

Eine weitere:

Das erste vollkommene Quadrat in der Fibonacci-Folge,144, ist in der Folge die Nummer 12 seine Quadratwurzel ist 12

0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144

oder   wir lassen die „ 0 “ weg und beginnen so:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144

 

Das Pascal’sche Dreieck:

Pascal hat dieses Zahlendreieck zwar nicht entdeckt (es war schon den Chinesen als Chu Shun Chiehs Dreieck bekannt), aber als erster systematisch untersucht. Die erste und letzte Zahl jeder Reihe ist 1; die übrigen Zahlen erhält man, indem man jeweils die beiden darüberstehenden Zahlen addiert:

 

1
1       1
1       2       1
1       3       3       1
1       4       6       4       1
1       5     10     10       5       1
1       6     15     20     15       6       1
1       7     21     35     35     21       7       1
1       8     28     56     70     56     28       8       1
1       9     36     84   126   126     84     36       9       1
1     10     45   120   210   252   210   120     45     10       1
1     11     55   165   330   462   462   330   165     55     11       1
1     12     66   220   495   792   924   792   495   220     66     12       1

Das pascalsche Dreieck ist eine Anordnung von Zahlen in Dreiecksform,konstruiert nach einem einfachen Bildungsgesetz, das wie folgt heißt:

„Man geht von einem Dreieck aus drei Einsen aus. Die folgenden Zeilen beginnen und enden auch mit einer Eins. Dazwischen liegen Zahlen, die sich als Summe der beiden darüber liegenden Zahlen ergeben. So kann das Dreieck nach unten hin beliebig weit fortgesetzt werden.“ Ich will Euch nicht mit den vielen Möglichkeiten die dass pascalsche Dreieck bietet, langweilen. Es ist jedoch interessant sich das mal anzuschauen, was so dahinter steckt, welche Aussagen getroffen werden. Wer dennoch mehr wissen will, klickt einfach auf die Verlinkung.

Kräfte von Phi und seinem Kehrwert:

Wir wissen:

Phi ² = Phi + 1

Diese Gleichung kommt dieser sehr nahe

Phi ² = Phi ¹ + Phi ⁰

Dies führt zu der Tatsache, das für jedes n gilt:

Phi ⁿ⁺² = Phi ⁿ⁺¹ + Phi ⁿ

folglich ist jede der 2 sukzessiven Kräfte addiert sich mit der Nachfolgenden.

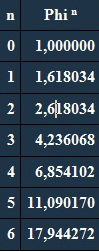
Kräfte von Phi:

Eine weiter Kuriosität ist, dass wenn man Phi als Kraft annimmt und diese mit seinem Kehrwert addiert oder subtrahiert:

Für jede gerade Zahl von n gilt:

Phi ⁿ  +  1 / Phi ⁿ = ergibt eine ganze Zahl

Für jede ungerade Zahl von n gilt:

Phi ⁿ  –  1 / Phi ⁿ = ist auch eine ganze Zahl