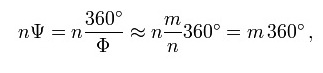Viele Pflanzen weisen in ihrem Bauplan Spiralen auf, deren Anzahl durch Fibonacci-Zahlen gegeben sind, wie beispielsweise bei den Samen in Blütenständen. Das ist dann der Fall, wenn der Winkel zwischen architektonisch benachbarten Blättern oder Samen bezüglich der Pflanzenachse der Goldene Winkel ist. Hintergrund ist der Umstand, dass die rationalen Zahlen, die den zugrunde liegenden Goldenen Schnitt am besten approximieren, Brüche von aufeinanderfolgenden Fibonacci-Zahlen sind. Die Spiralen werden daher von Pflanzenelementen gebildet, deren Platznummern sich durch die Fibonacci-Zahl im Nenner unterscheiden und damit fast in die gleiche Richtung weisen. Durch diese spiralförmige Anordnung der Blätter um die Sprossachse erzielt die Pflanze die beste Lichtausbeute. Der Versatz der Blätter um das irrationale Verhältnis des Goldenen Winkels sorgt dafür, dass nie Perioden auftauchen, wie es z. B. bei 1/4 der Fall wäre (0° 90° 180° 270° | 0° 90° …). Dadurch wird der denkbar ungünstigste Fall vermieden, dass ein Blatt genau senkrecht über dem anderen steht und sich so die jeweils übereinanderstehenden Blätter maximalen Schatten machen oder maximale ‚Lichtlücken‘ entstehen.
Ursache ist das Bestreben dieser Pflanzen, ihre Blätter auf Abstand zu halten. Es wird vermutet, dass sie dazu an jeder Blattwurzel einen besonderen Wachstumshemmer erzeugt, der im Pflanzenstamm – vor allem nach oben, in geringerem Umfang aber auch in seitlicher Richtung – diffundiert. Dabei bilden sich in verschiedene Richtungen bestimmte Konzentrationsgefälle aus. Das nächste Blatt entwickelt sich an einer Stelle des Umfangs, wo die Konzentration minimal ist. Dabei stellt sich ein bestimmter Winkel zum Vorgänger ein. Würde dieser Winkel den Vollkreis im Verhältnis einer rationalen Zahl \tfrac{m}{n} teilen, dann würde dieses Blatt genau in die gleiche Richtung wachsen wie dasjenige n Blätter zuvor. Der Beitrag dieses Blattes zur Konzentration des Inhibitors ist aber an dieser Stelle gerade maximal. Daher stellt sich ein Winkel mit einem Verhältnis ein, das alle rationalen Zahlen meidet. Die Zahl ist nun aber gerade die Goldene Zahl (siehe oben). Da bisher kein solcher Inhibitor isoliert werden konnte, werden auch andere Hypothesen diskutiert, wie beispielsweise die Steuerung dieser Vorgänge in analoger Weise durch Konzentrationsverteilungen von Nährstoffen.
Bei vielen nach dem Goldenen Schnitt organisierten Pflanzen bilden sich in diesem Zusammenhang so genannte Fibonacci-Spiralen aus. Spiralen dieser Art sind besonders gut zu erkennen, wenn der Blattabstand im Vergleich zum Umfang des Pflanzenstammes besonders klein ist. Sie werden nicht von aufeinander folgenden Blättern gebildet, sondern von solchen im Abstand n, wobei n eine Fibonacci-Zahl ist. Solche Blätter befinden sich in enger Nachbarschaft, denn das n-fache des Goldenen Winkels Ψ ist ungefähr ein Vielfaches von 360° wegen

wobei m die nächst kleinere Fibonacci-Zahl zu n ist. Da jedes der Blätter zwischen diesen beiden zu einer anderen Spirale gehört, sind n Spiralen zu sehen. Ist \tfrac{n}{m} größer als Φ so ist das Verhältnis der beiden nächsten Fibonacci-Zahlen kleiner und umgekehrt. Daher sind in beide Richtungen Spiralen zu aufeinander folgenden Fibonaccizahlen zu sehen. Der Drehsinn der beiden Spiralentypen ist dem Zufall überlassen, sodass beide Möglichkeiten gleich häufig auftreten.

Pflanzen zeigen die Fibonacci-Reihe in der Anzahl und Anordnung der Blütenblätter, Blätter, Abschnitte und Samen. Pflanzen, die in Spiralen, wie Tannenzapfen, Ananas und Sonnenblumen wachsen, stellen ebenso die Fibonacci-Zahlen dar. Fibonacci-Zahlen in einer Pflanzenspirale:

Hier ein Sonnenblumenkern dieses Prinzip in der Anzahl der rechtsdrehenden Spiralen – Gesamtzahl: 55 (rot markiert, jede zehnte ist mit Weiß markiert). Die Zahl der gegen Uhrzeigersinn drehenden Spiralen ist 89 (grün markiert, mit jede zehnte in weiß.)

Die beiden ersten Blätter einer Sonnenblume stehen sich noch genau gegenüber. Je mehr Blätter wachsen, desto mehr scheint jedoch auch die Ordnung in der Anordnung der Blätter verloren zu gehen. Die Blätter stehen in vermeintlich beliebige Richtungen auseinander. Diese Art chaotisches Wachstum setzt sich bis in die Blüte hinein fort. Dort jedoch zeichnet sich ein Muster ab. Statt Chaos und beliebiger Anordnung deutet hier alles auf Ordnung und System hin. Deutlich zu erkennen sind Spiralmuster (Parastichen genannt). Meistens lassen sich zwei gegenläufige Parastichenserien unterscheiden. Zählt man die Parastichen in jeder Richtung (mit und gegen den Uhrzeigersinn), erhält man Zahlenpaare der Fibonacci-Reihe. Die nächste Zahl entspricht stets der Summe der beiden vorherigen Zahlen – und die Verhältnisse der aufeinander folgenden Zahlenpaare nähern sich dem Goldenen Schnitt an.

Das Keimzentrum lässt den jeweils nächsten Samen (oder an einem Stängel das jeweils nächste Blatt bzw. den jeweils nächsten Seitentrieb) immer um den Goldenen Winkel 137.50 versetzt entstehen.

Ein Erklärungsversuch für dieses Auftreten der Fibonacci-Zahlen ist vielleicht, dass die Blattstellung im Winkel des Goldenen Schnitts (im Goldenen Winkel) deshalb so optimal ist, weil das Wachstum von Blättern bekanntlich durch Beschattung begrenzt ist, und so sicher gestellt wird, das jedes einzelne Blatt einen guten Anteil an Licht bekommt. Bei den Blüten garantiert diese Anordnung, dass die größtmögliche Anzahl von Samenkörnern auf einer so klein wie möglichen Fläche zusammengepackt werden kann. Schon geringe Abweichungen vom Goldenen Schnitt würden dazu führen, dass der verfügbare Platz auf dem Blütenboden nicht mehr optimal genutzt werden könnte.

Die Schuppen von Fichtenzapfen, wie auch von Ananasfrüchten bilden im und gegen den Uhrzeigersinn Spiralen, deren Schuppenanzahl durch zwei aufeinanderfolgende Fibonaccizahlen gegeben ist.

.
(Tannenzapfen mit 5, 8 und 13 Fibonacci-Spiralen)

Fibonacci-Zahlen in den Verzweigungen:

Hier wird anschaulich dargestellt, dass jede nachfolgende Ebene der Zweigstellen oft auf eine Progression durch die Fibonacci-Reihe basiert.

Sie könnten Symmetrie in Pflanzen erwarten, aber wenn Sie Obst oder Gemüse schneiden, werden Sie häufig feststellen, dass die Zahl von Abschnitten oder Unterteilungen eine Fibonacci-Zahl ist:

Bananen haben 3